^ mapForm bits count: [ :bit |
       (Color colorFromPixelValue: bit depth: 32) green
       closeTo: 1
       precision: 0.1 ]

Hi all, I remember to read in the Blue Book about a Game Of Life solution based on the BitBlt operation. I wondered if it was only a smart and elegant demonstration or it may be a useful tool in the case you need parallelism, even in non-graphical contexts. I've never seen BitBlt used to solve non-graphical problems, but I don't have experience with BitBlt in my everyday work, so maybe I'm biased. I've found a paper by Leo J. Guibas and Jorge Stolfi ( https://www.cs.tufts.edu/~nr/cs257/archive/leo-guibas/language-bitmap.pdf) about a "calculus of bitmap operations" including an specific language called MUMBLE, but I suspect it is not a common use case. Anyway, I've experimented with this option to solve the Advent of Code's Day 3 challenge. The puzzle consists of counting the number of trees you will encounter traversing a given map with open squares and trees, starting at the top-left corner and following a certain slope (( https://adventofcode.com/2020/day/3). 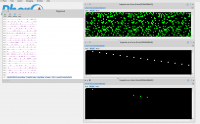After implementing the straight-forward and iterative solution, I tried using Form instances representing the map and the slope and a BitBlt operation for ANDing both forms in order to leave only bits where you encounter a tree (see attached image). In this alternative solution I like how the iteration is replaced by only one "BitBlt>>copyBits" operation. Additionally, I understand that BitBlt operations are native primitives that could be hardware optimized. However, I didn't know how to count the resulting bits without recurring again to the iteration of the Form's bits. This is my current implementation: AoCBitBltForestMap>>countTreesOnPath | mapForm | mapForm := self form. (BitBlt toForm: mapForm) copyForm: self slopeMaskForm to: 0 @ 0 rule: Form and. ^ mapForm bits count: [ :bit | (Color colorFromPixelValue: bit depth: 32) green closeTo: 1 precision: 0.1 ] You can find all the sources at the following repository: https://github.com/luque/AdventOfCode2020 Any comments about BitBlt use cases or this specific puzzle will be of interest for me. Thank you.

 ^ mapForm bits count: [ :bit | 
        (Color colorFromPixelValue: bit depth: 32) green
        closeTo: 1
        precision: 0.1 ]

I do not have your answer but I see that you are having fun… :) Continue. I’m playing with VM implementation for the exact same reason :) > On 21 Dec 2020, at 10:56, Rafael Luque <rafael.luque.leiva@gmail.com> wrote: > > Hi all, > > I remember to read in the Blue Book about a Game Of Life solution based on the BitBlt operation. I wondered if it was only a smart and elegant demonstration or it may be a useful tool in the case you need parallelism, even in non-graphical contexts. I've never seen BitBlt used to solve non-graphical problems, but I don't have experience with BitBlt in my everyday work, so maybe I'm biased. > > I've found a paper by Leo J. Guibas and Jorge Stolfi (https://www.cs.tufts.edu/~nr/cs257/archive/leo-guibas/language-bitmap.pdf <https://www.cs.tufts.edu/~nr/cs257/archive/leo-guibas/language-bitmap.pdf>) about a "calculus of bitmap operations" including an specific language called MUMBLE, but I suspect it is not a common use case. > > Anyway, I've experimented with this option to solve the Advent of Code's Day 3 challenge. The puzzle consists of counting the number of trees you will encounter traversing a given map with open squares and trees, starting at the top-left corner and following a certain slope ((https://adventofcode.com/2020/day/3 <https://adventofcode.com/2020/day/3>). > > After implementing the straight-forward and iterative solution, I tried using Form instances representing the map and the slope and a BitBlt operation for ANDing both forms in order to leave only bits where you encounter a tree (see attached image). In this alternative solution I like how the iteration is replaced by only one "BitBlt>>copyBits" operation. Additionally, I understand that BitBlt operations are native primitives that could be hardware optimized. > > However, I didn't know how to count the resulting bits without recurring again to the iteration of the Form's bits. This is my current implementation: > > AoCBitBltForestMap>>countTreesOnPath > | mapForm | > mapForm := self form. > (BitBlt toForm: mapForm) > copyForm: self slopeMaskForm > to: 0 @ 0 > rule: Form and. > > ^ mapForm bits count: [ :bit | > (Color colorFromPixelValue: bit depth: 32) green > closeTo: 1 > precision: 0.1 ] > > You can find all the sources at the following repository: https://github.com/luque/AdventOfCode2020 <https://github.com/luque/AdventOfCode2020> > > Any comments about BitBlt use cases or this specific puzzle will be of interest for me. > > Thank you. > > > > > <Captura de pantalla 2020-12-21 a las 10.50.26.png> -------------------------------------------- Stéphane Ducasse http://stephane.ducasse.free.fr / http://www.pharo.org 03 59 35 87 52 Assistant: Aurore Dalle FAX 03 59 57 78 50 TEL 03 59 35 86 16 S. Ducasse - Inria 40, avenue Halley, Parc Scientifique de la Haute Borne, Bât.A, Park Plaza Villeneuve d'Ascq 59650 France